[Algorithm] Single-Source Shortest Path : Bellman-Fold, DAG, Dijkstra

Shortest Path

• 관련 용어
  • input : weighted, directed graph G
  • path p : 노드 리스트 <v0, v1, … , vk>
  • distance : edge weight w(p)
  • shortest path weight $\delta$(u, v) : u, v로 가는 경로 중 min weight (길 없으면 $\infin$)
• 관련 정의
  • Shortest path 의 subpath는 모두 Shortest path
  • negative weight cycle이 존재할 경우, shortest path 정의할 수 없다.
    • negative weight cycle은 cycle의 weight의 합이 음수인 경우
    • negative weight cycle이 존재할 경우, 이 부분을 무한히 돌면 shortest weight가 무한히 감소한다.

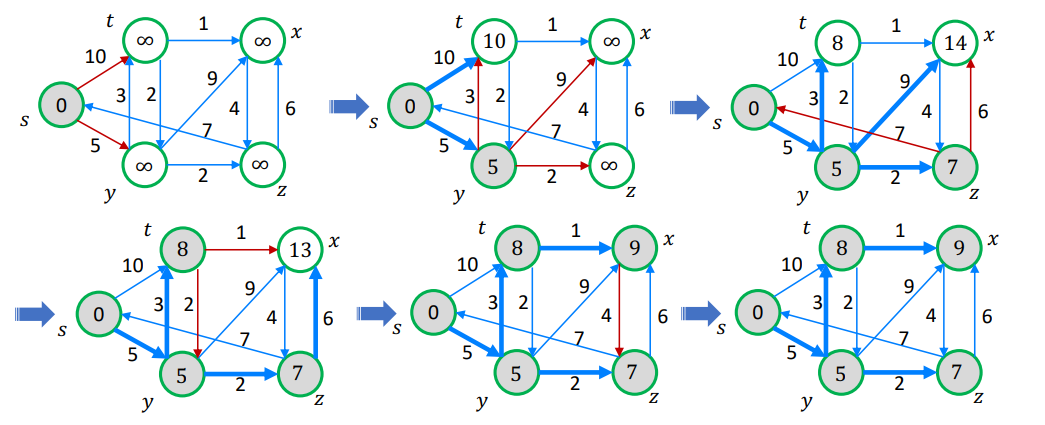
Single Source Shorstest Path

• : 주어진 한 vertex를 source로 해서, 다른 모든 vertex까지의 shortest path 찾기
• tree와 유사한 구조
• ununique - 동일 weight 존재 가능

• 노드 별로 shortest distance d와 parent $\pi$로 구성

  

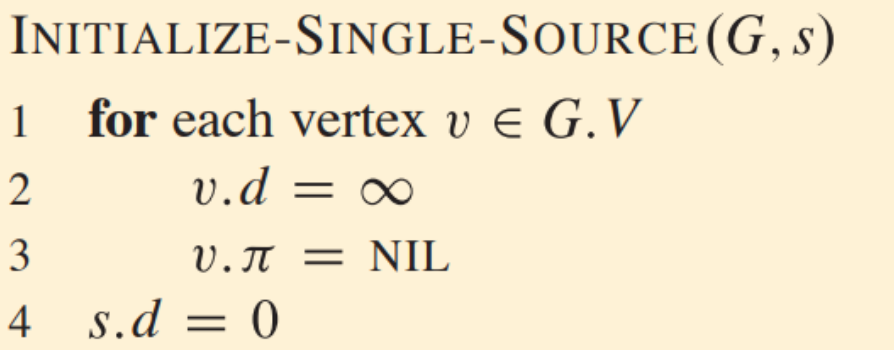
Bellman-Fold Algorithm

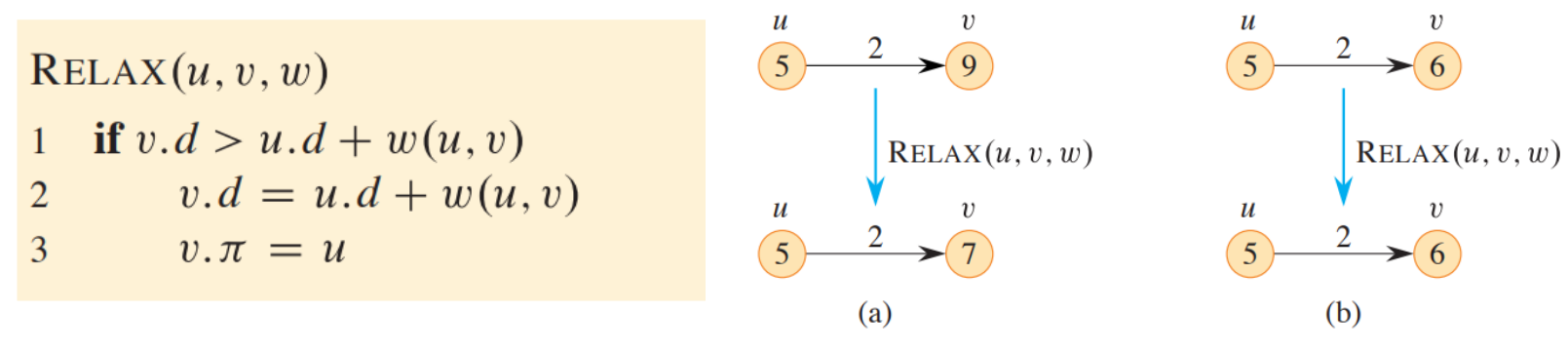
• relax 통해 진행

  • 앞 단계 노드 d + edge weight가 더 작으면 d update

    

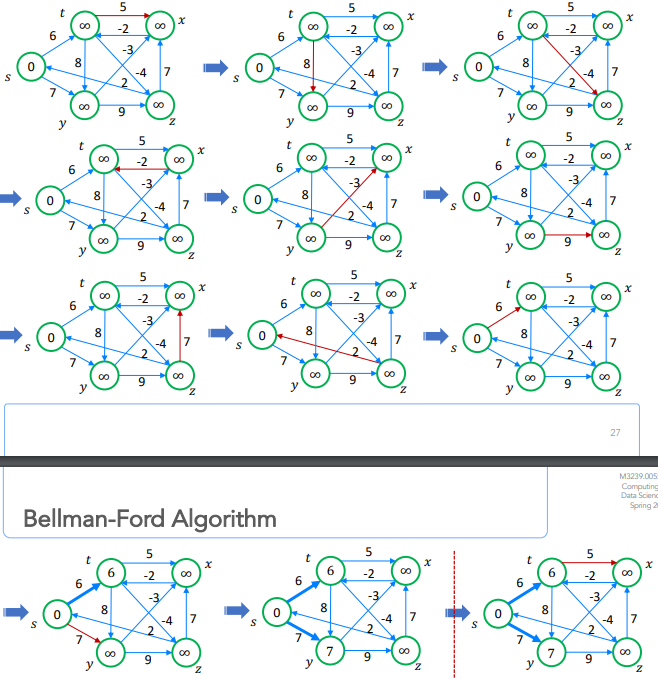
• V-1 번, 모든 edge를 relax
  • 끝난 후엔 cycle 유무 확인(다시 도는데 또 update 할 게 남아있으면, cycle)

  

• complexity : O(VE)

• 예시

  

DAG(Directed Acyclic Graph) Shortest Paths

• 방법 : topological sort 정렬 후, 차례로 돌며 adjacent edge들만 relax

  

• 예시

  

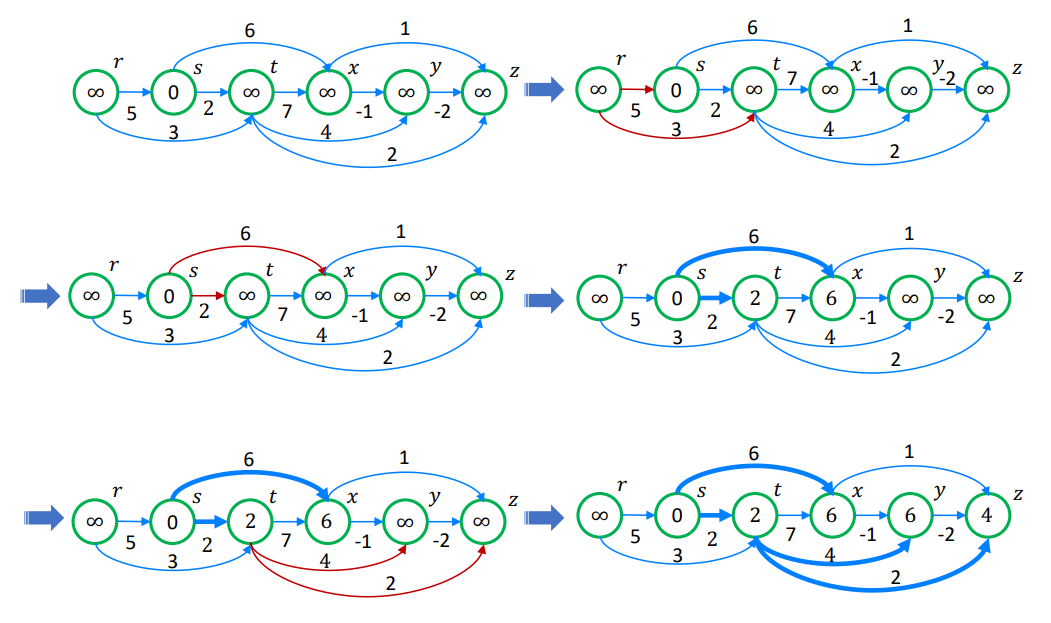
Dijkstra’s Algorithm

• non-negative weight 가정
• 방법
  • 1) source를 Q에 넣는다
  • 2) Q에서 min node를 빼고, return node의 인접 노드들을 relax 후 Q에 넣기

  

• 예시