[Algorithm] Minimum Spanning Tree(MST) Problem : Cut, Prim’s, Kruskal’s

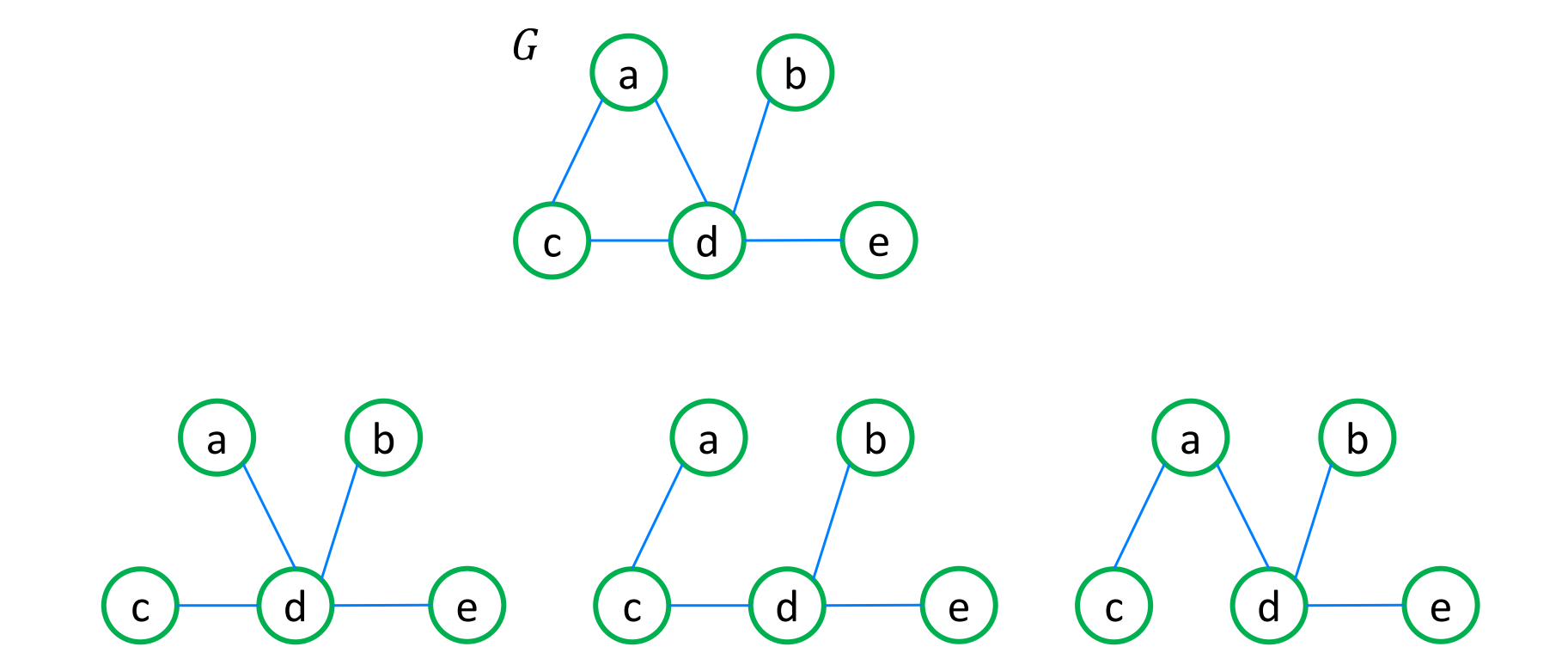
• Spanning Tree

  : 모든 vertex를 포함하고, undirected이며, cycle이 없는(Tree) SubGraph

  

• MST

  : total weight가 가장 작은 spanning tree

  

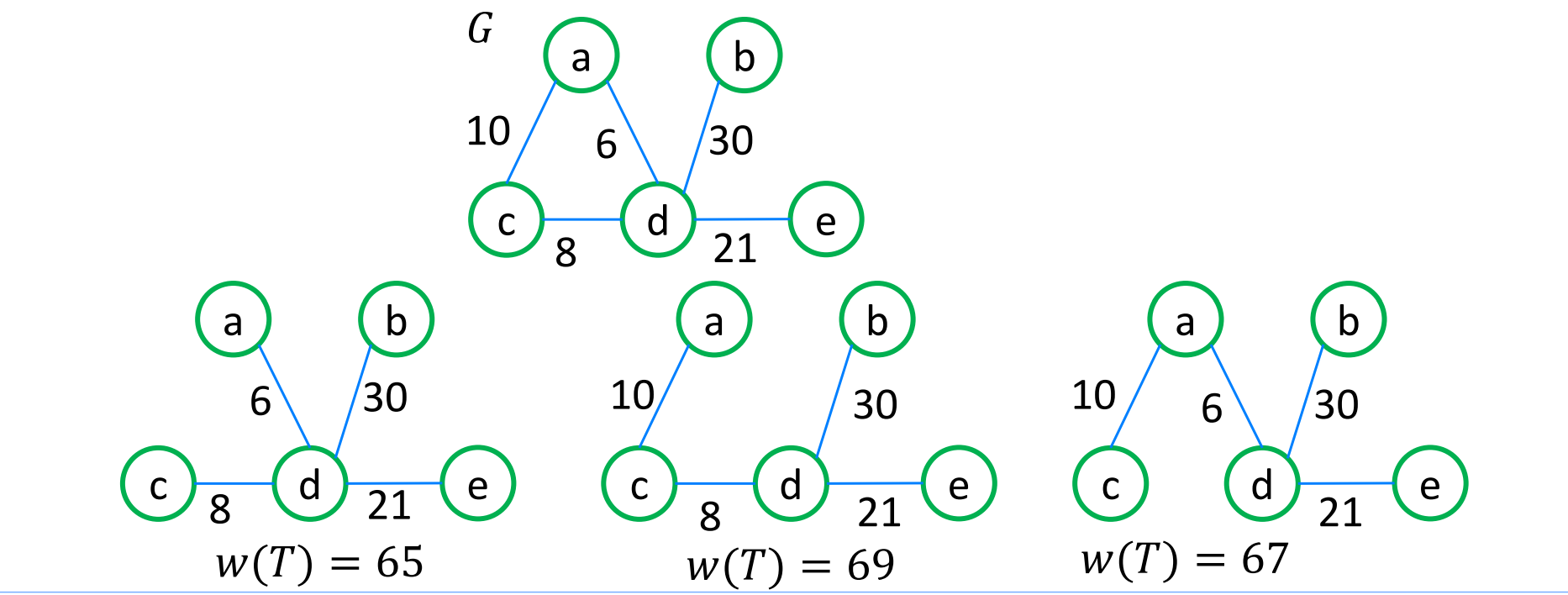
  • not be unique
    • 모든 edge의 weight가 각각 다르다는 가정에서만 unique

• MST Problem

  • connected, weighted, undirected graph G가 주어졌을 때, G의 MST를 찾는 것
  • 방법
    • empty tree로 시작
    • safe edge(MST의 subset인 edge)들을 하나씩 더하며 만들기
      • weight 작고, acyclic

Greedy Algorithm with Cut

• Greedy Algorithm 이란
  • 차례대로 돌며, 각 순간의 best를 고르는 방식
  • global optimal을 보장하지 않지만, 간단하고 효율적이다.
  • MST에선 충분히 유용하다.
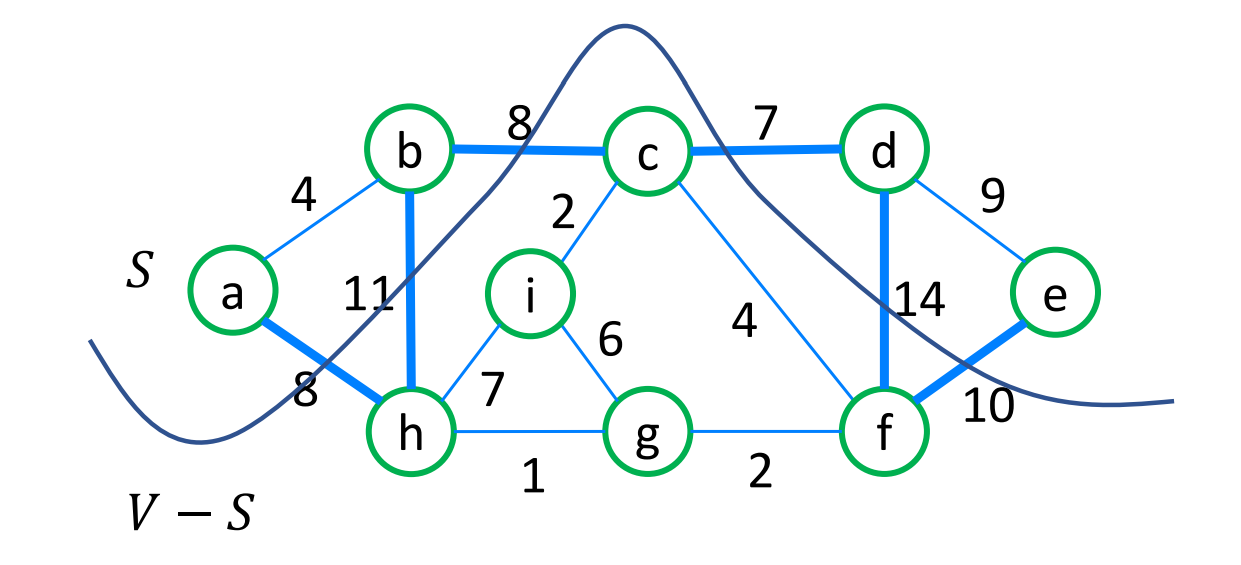
• Cut이란
  • G의 vertex들을 (S, V-S)로 나누는 선
  • cut을 지나는 edge 중 minimum weight 가지면, safe edge로 선택

Prim’s Algorithm

• 방법
  • Adjacency list 가 linked list 형태로 주어진다고 가정
  • 1) 임의의 vertex 골라서 root로 tree에 넣기
  • 2) tree에 연결된 edge 중 minimum weight edge와 연결된 vertex를 tree에 더한다.
    • mim-priority queue 활용 가능(필수 x)
      • key(연결 가능한 edge 중 min 값)와 $\pi$(parent)를 가지는 node를 넣음
    • 이미 tree에 포함되지 않은 edge와 vertex 여야 한다.

• 예시

  

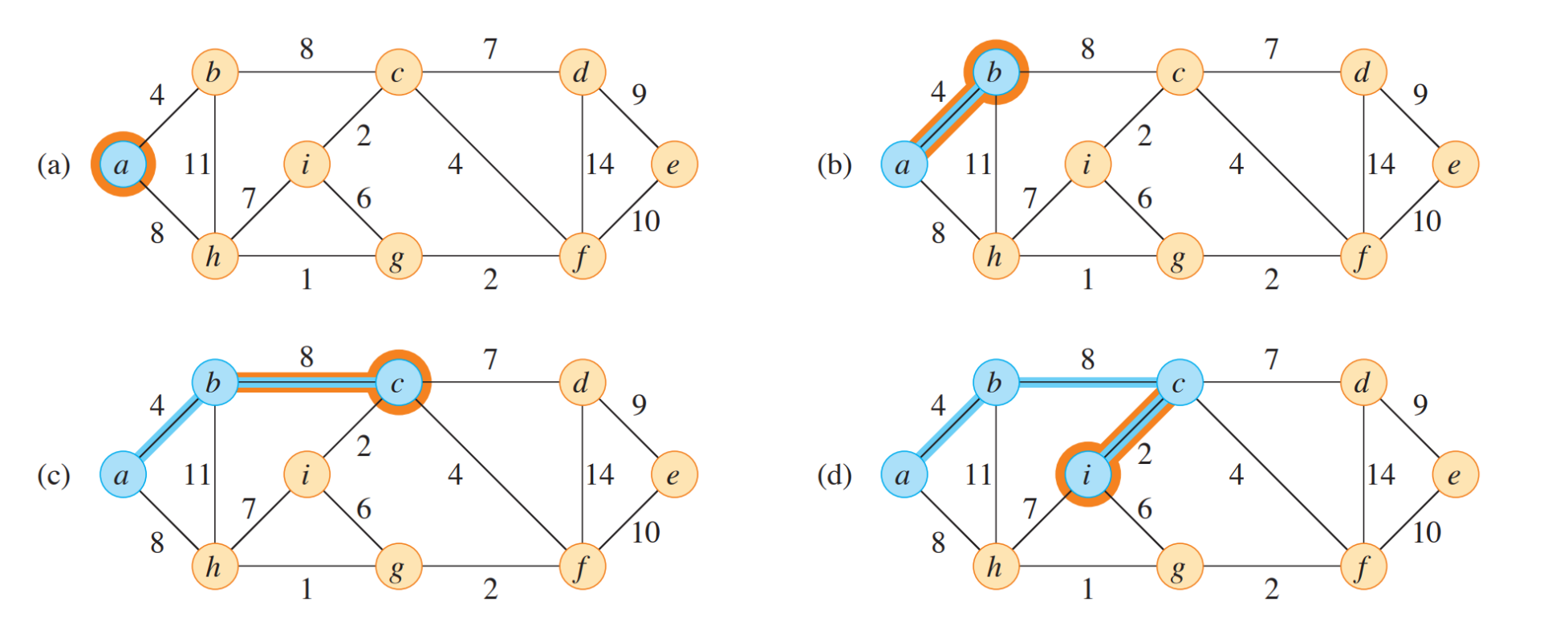
• Pseudo Code

  

• complexity : O((E+V)lgV)
  • extract Queue O(lg n) * num of vertex V
  • decrease key O(lg n) * num of edge E

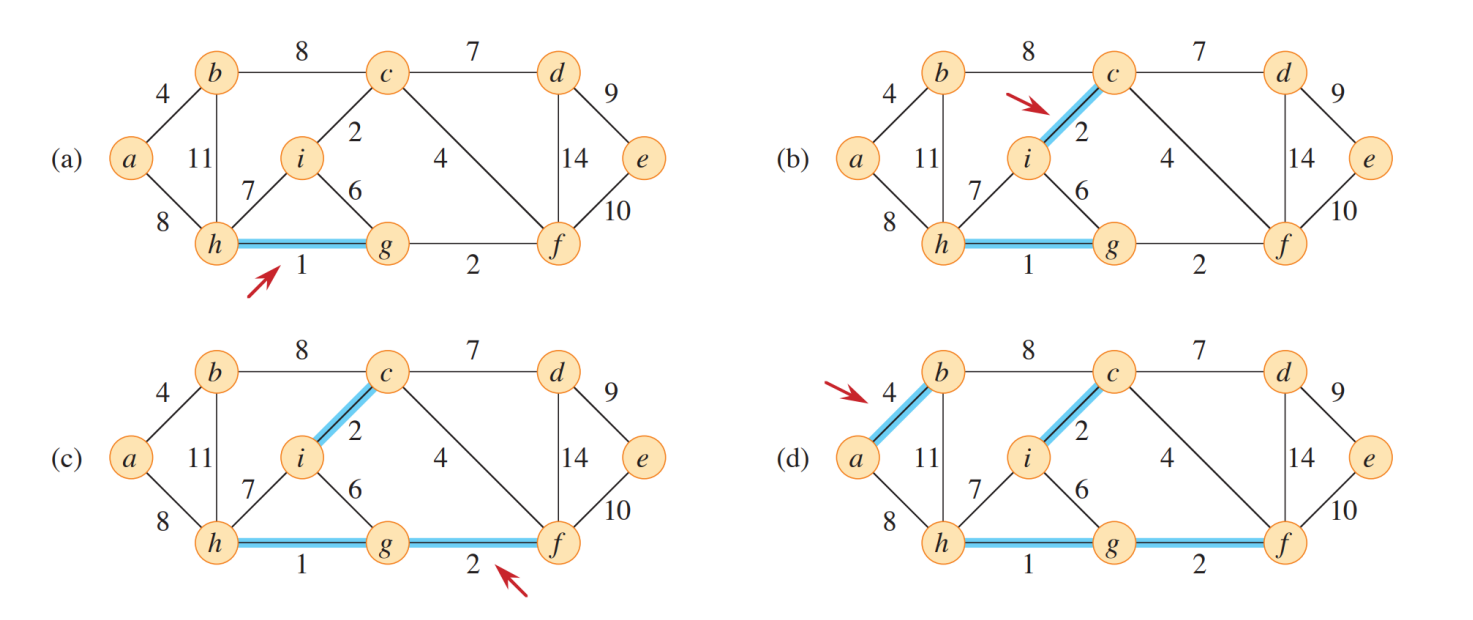
Kruskal’s Algorithm

• 매번 minimum weight edge 선택 + cycle 생기는지 여부 check

• Pseudo Code