1 분 소요

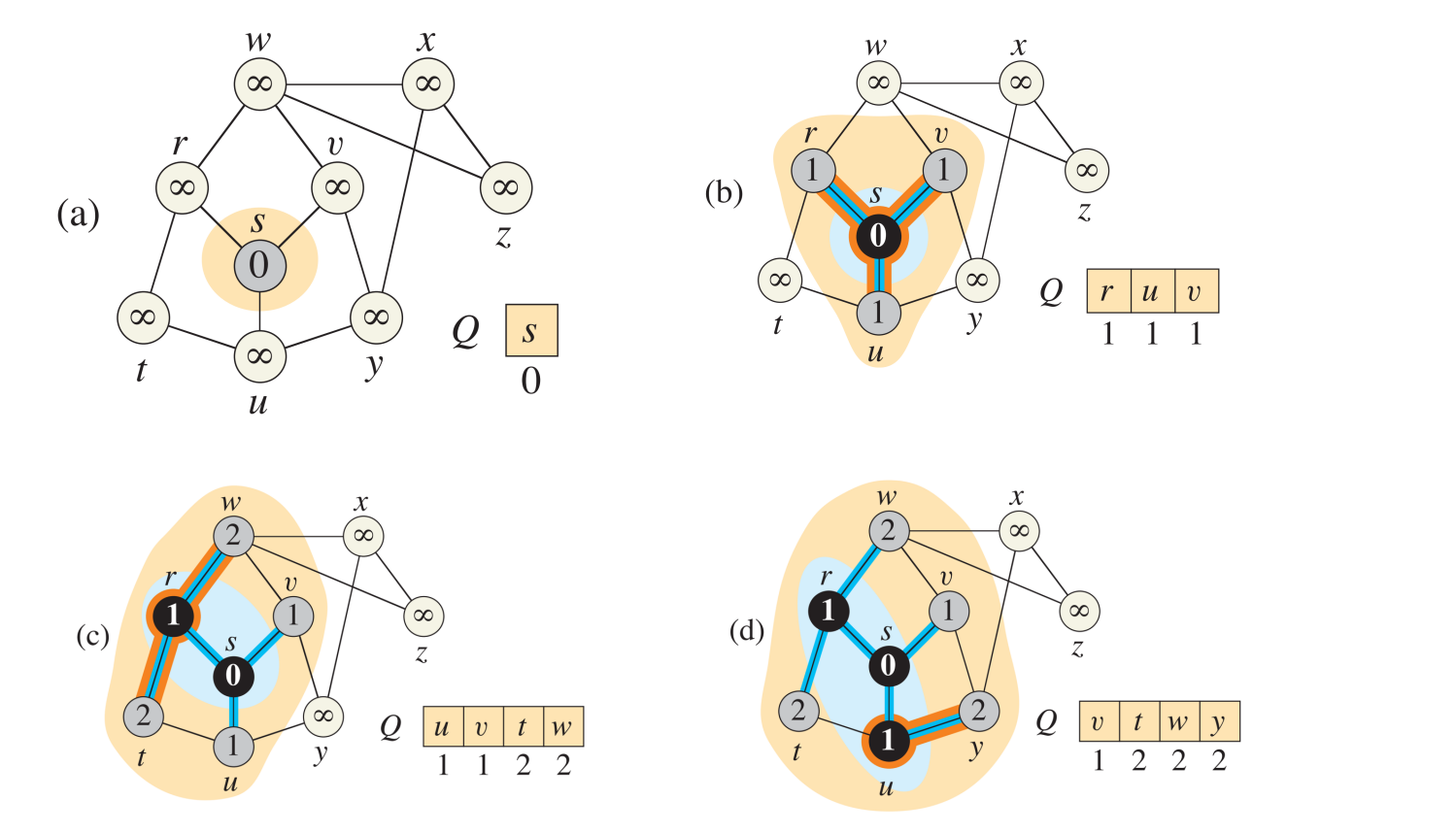
BFS : Breadth First Search 넓이 우선 탐색

  • 사용 목적 : shortest path 찾기
  • 방법
    • vertex에 color 개념 활용
      • white : 방문 안 함, init 상태
      • gray : 1번 방문, Queue에 입력
      • black : 2번 방문, Queue에서 출력, 연결된 vertex들은 모두 1번 이상 방문 상태
    • source 지정해서 시작
  • 예시

Untitled

  • Pseudo Code

    Untitled

  • Complexity : $O(V+E)$

    • init : $\theta(V)$
    • 본격 bfs : 각 노드 별로 자신의 edge들 방문. linked list 구현 시, 전체 edge 수 만큼만 방문하게 됨.

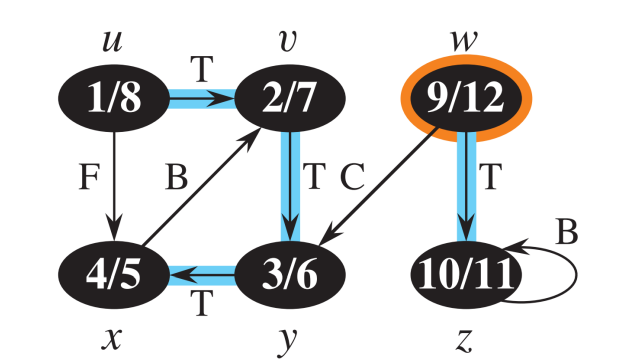
DFS : Depth First Search 깊이 우선 탐색

  • only directed graph
  • 목적 : topological sort 등 다른 algorithm의 subroutine으로 사용
  • 방법
    • source 지정 없이, 랜덤한 노드에서 시작

  • 예시

    Untitled

  • Pseudo Code

    Untitled

DFS 활용 : Topological Sort

  • DAG(Directed Acyclic Graph)에서 다른 노드 간의 logical 순서 찾기
  • 방법 : DFS의 Finish Time 순으로 linked list 앞에 넣기
  • 항상 같은 순서 x. 하지만 관련된 2개 간의 선후가 바뀌진 않음

DFS 활용 : Strongly Connected Component

  • cycle을 이루게 되는 묶음
  • a→b로 가는 경로가 있을 때, b→a로 가는 경로도 있으면 a와 b는 strongly connected

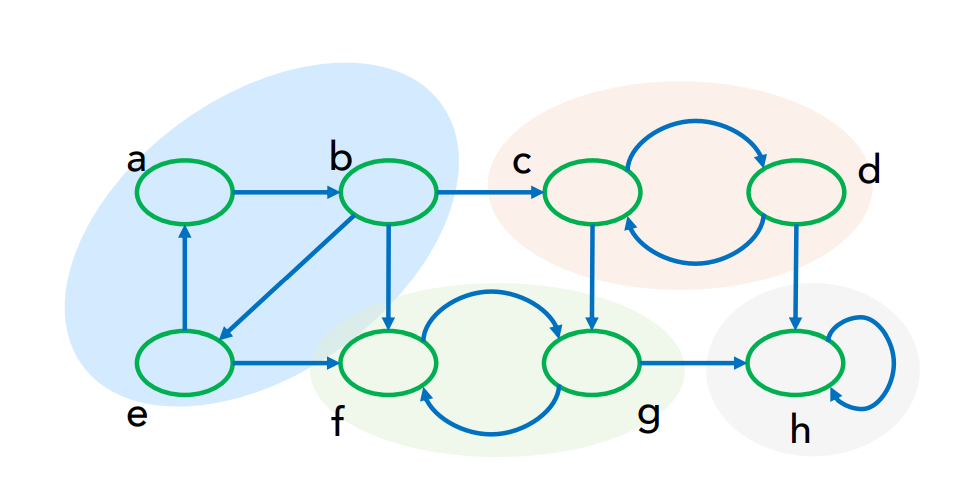
Untitled

  • Graph Transpose 통해 구할 수 있다.

    • GraphTranspose : 모든 E의 방향만 바꾼다.

      \[E^T = \{(u, v) : (v, u) \in E \}\]
    • E와 $E^T$는 같은 strongly connected component를 갖는다.

    • Strongly Connected Component 찾기

      1) DFS(G)

      2) $G^T$ 만들기

      3) G의 마지막 노드에서부터 시작해서, $G^T$의 DFS 수행.

      이때, 할 것이 없어서 연결이 끊기로, 새로 random한 수행 필요할 때까지가 Stronly Connected Component

  • Component Graph

    • strongly connect component끼리 묶어서 하나의 노드 취급하여, 새로운 그래프 만들기

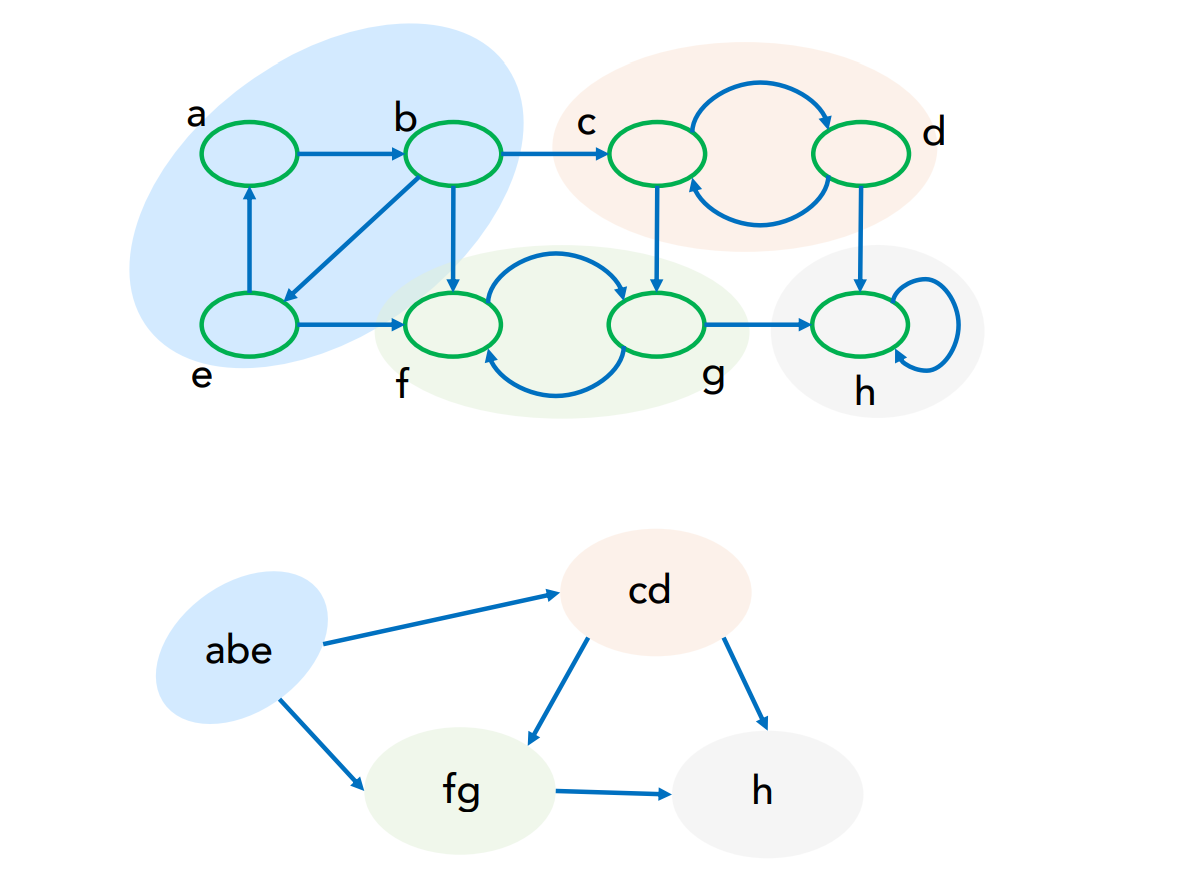
      Untitled

    • 여기선 같은 노드간의 →가 있으면, 그 역은 없다.
    • c’ →c 이면, finish time f(c’) > f(c)