[Algorithm] Dynamic Programming

Divide and Conquer

• 전체를 작은 subproblem으로 나눠서, 작은 문제를 푼 후 합치는 기법
• recursively 수행

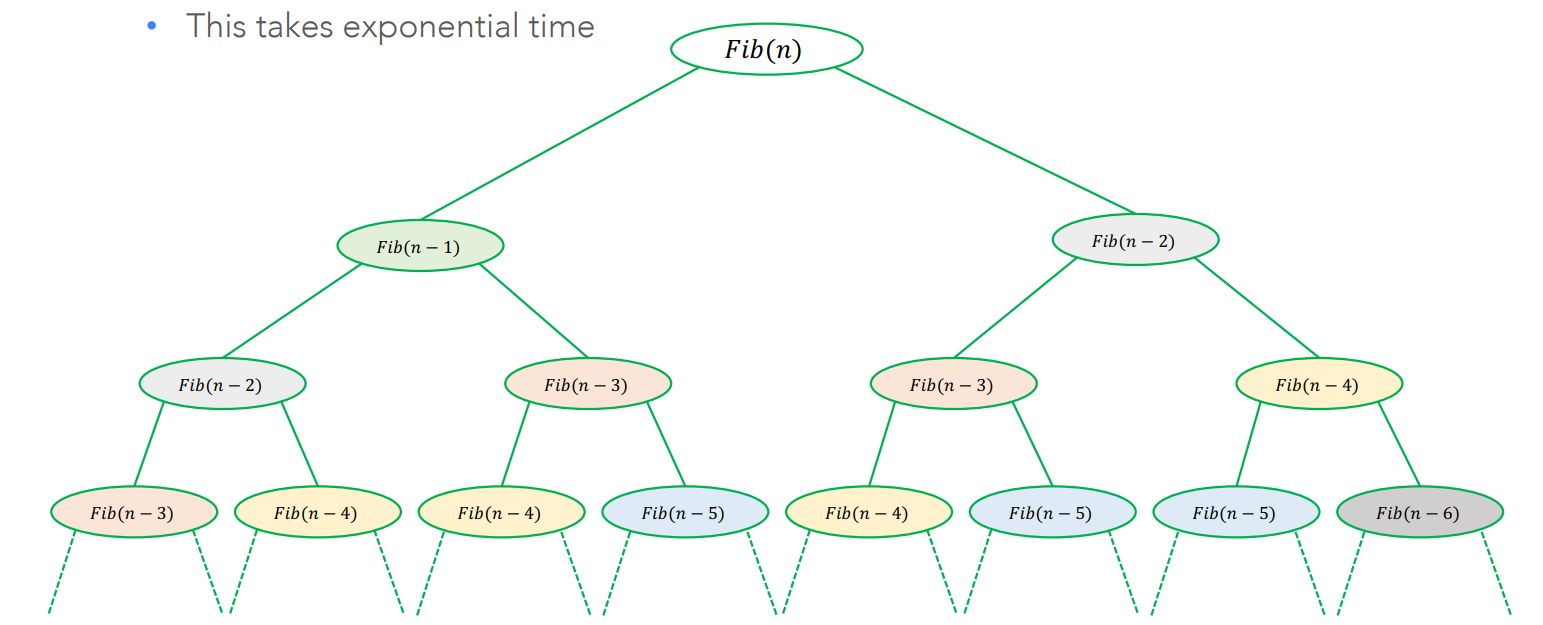
• 문제 : 중복 계산 많음 → Dynamic Programming

Dynamic Programming

• Divide & Conquer 기반 + 중복 계산 문제를 개선
• DAG(Directed Acyclic Graph)처럼 표현 가능

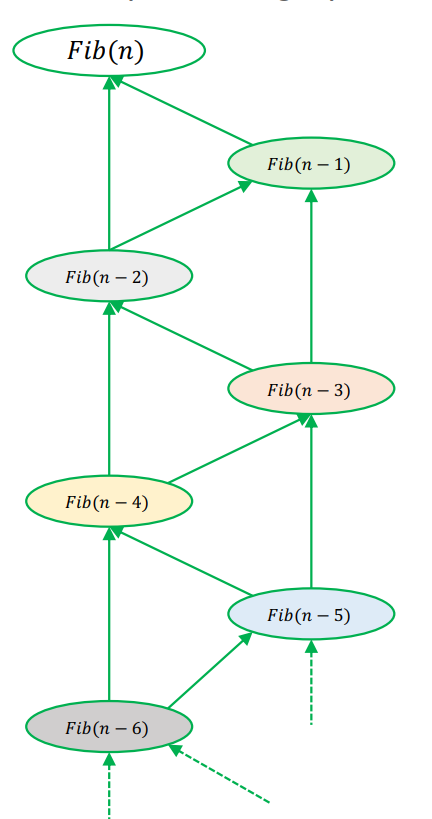
• Source → Destination
  • source : 가장 작은 subtree, 시작점, tree의 reaf, ex) Fib(1)
  • destination : 최종 목적, tree의 root, ex) Fib(n)
• 방법 : Memorization
  • 앞서 계산한 단위를 r[n]에 기록해두고, 다음에 필요할 때 그대로 사용

예 : Cut Rod

• Psuedo Code

  • Top-Down Approach

    

    

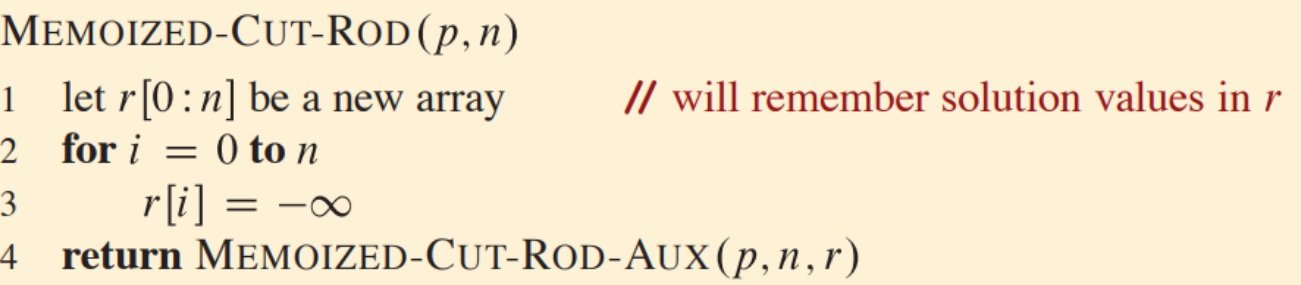
  • Bottom-up Approach
    • recursive 아님
    • 속도 동일하지만 구현이 더 간단해서 더 많이 사용

    

  • 자리는 방법까지 찾기
    • 앞선 코드는 최종 max 값만 찾음. 여기선 best 자르는 방법까지 저장

    

    • 8만 추가된 것
• Complexity
  • navie : call $2^n$
  • DP : $\theta(n^2)$
    • 각 subproblem들은 1번씩만 계산
    • 1+2+3 + … + n