[Algorithm] 자료구조2 : BST, RBT (1)
BST (Binary Search Tree)
-
항상
왼쪽 노드 <= 오른쪽 노드인 Binray Tree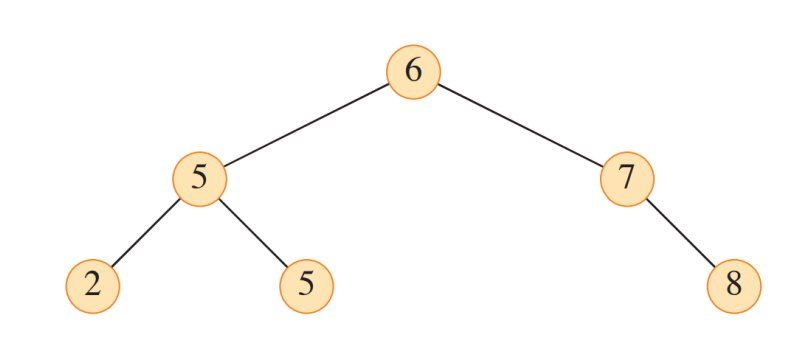
- 일종의 prority queue이기도 한 듯
- 기능
- inorder tree walk : 순서대로 출력
-
위 예시에서 수행 시,
2 5 5 6 7 8
-
- searching
- recursive와 iterative 방법 모두 가능
-
보통 더 빠른 iterative 사용

- Max, Min 찾기
-
계속 오른쪽/왼쪽으로 가기
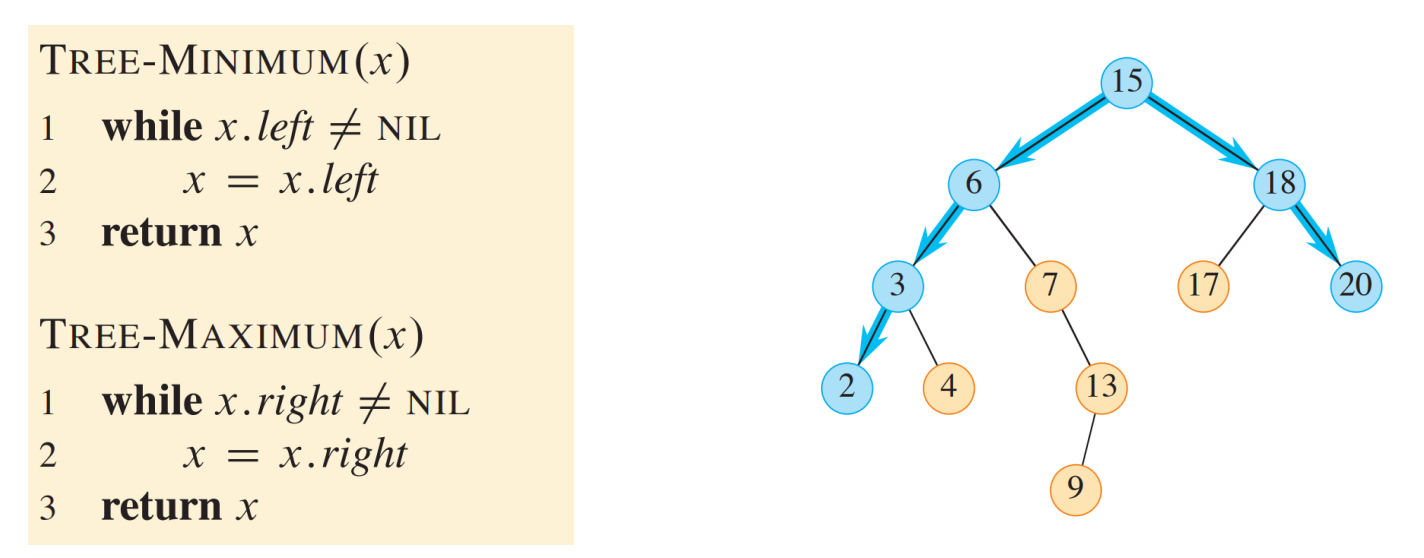
-
- Successor, Predecessor 찾기
- Successor : 나 다음으로 큰 값, 나보다 큰 값 중 가장 작은 값
- (root에서 시작 제외) 조상을 계속 따라가다가, 내가 부모의 left child 일 때의 부모
- Predecessor : 나 다음으로 작은 값, 나보다 작은 값 중 가장 큰 값
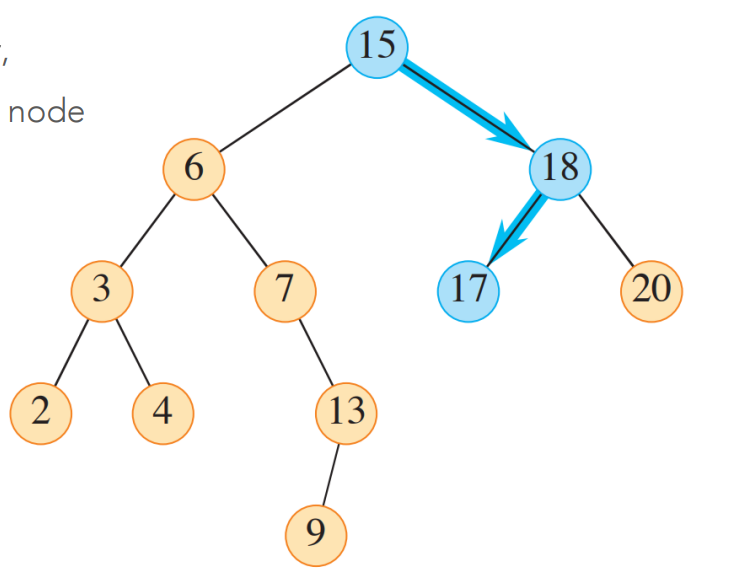
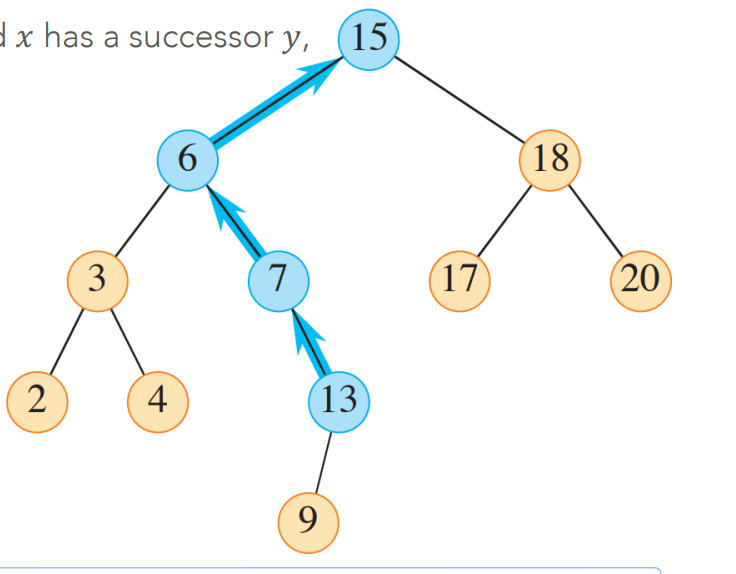
- Successor : 나 다음으로 큰 값, 나보다 큰 값 중 가장 작은 값
- insertion
- root부터 시작해서, key 비교해서 따라가다가 NIL이면 거기 삽입

- Deletion
- case1 : no children
- parent의 child를 NIL로 바꾸기
- case2 : one children
- 내 parent와 내 child를 연결(with 포인터)
- case3 : two children
-
successor를 내 자리에 넣기
1) successor의 child와 parent를 연결, successor는 successor의 parent의 parent로 만들기
2) successor를 내 parent와 연결
3) successor를 내 left child와 연결
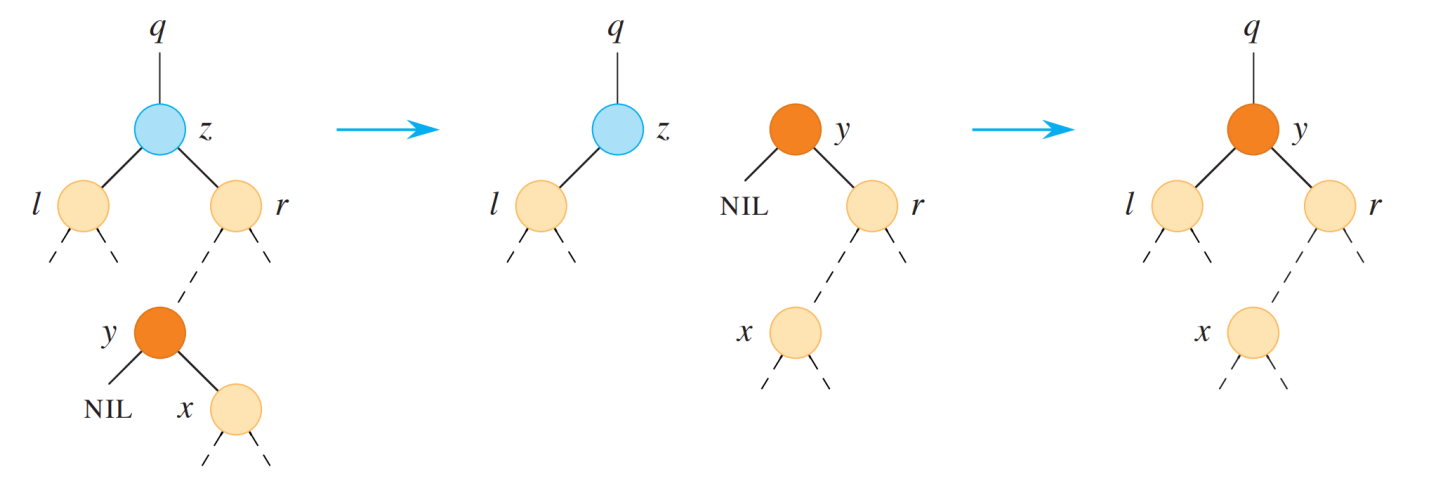
-

case1은 자식이 NIL 인 것과 같으므로, case 1, 2는 묶어서 수행
- transplant
-
이름은 바꾼다지만, 역할로는 연결로 보는 게 더 적절해 보임

-
- case1 : no children
- inorder tree walk : 순서대로 출력
RBT (Red-Black Tree)
- 특징
- BST의 일종
- BST에 비해, 어느 정도 balance를 유지 → 속도 향상
- 더 엄격한 균형 트리(ex AVL)는 최악의 경우 rotation이 훨씬 늘어날 수 있다.
-
균형 유지 방법 : rotation
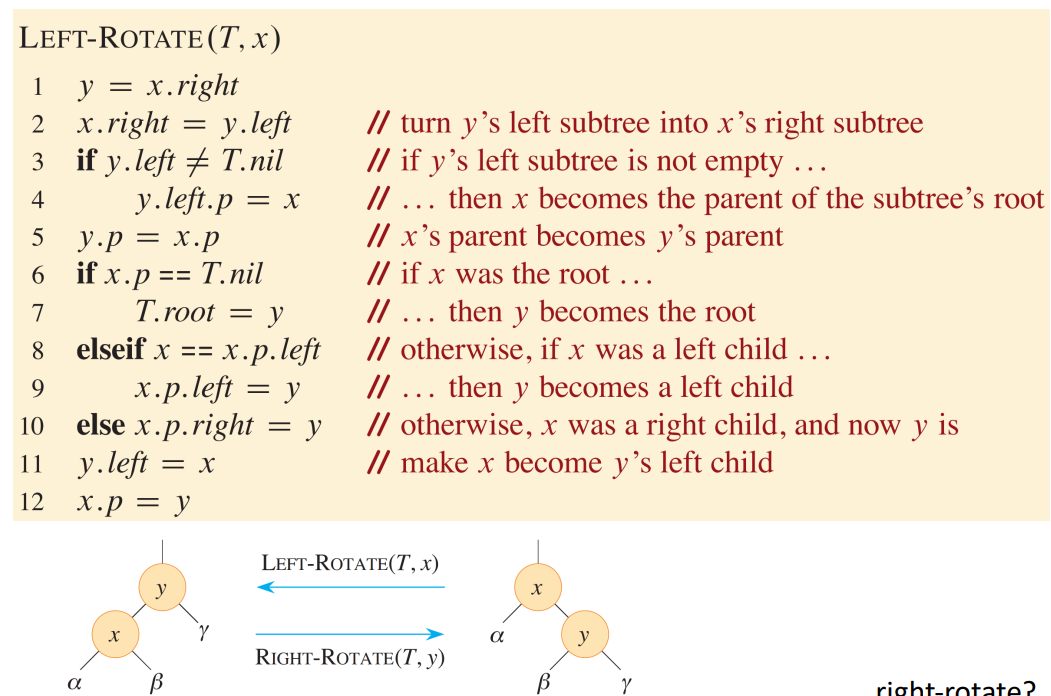
-
RBT properties

- 추가 특징(위 특징에서 파생)
- black node가 only one child 갖는다면, the child는 red node
- 추가 특징(위 특징에서 파생)
- 예시
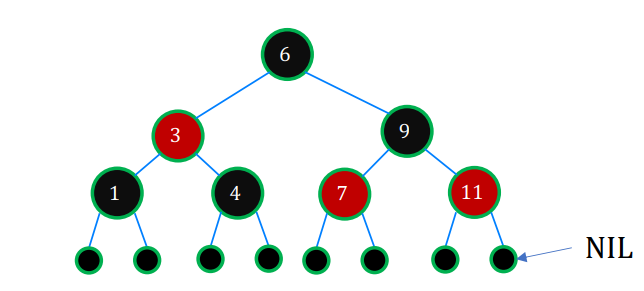
- 관련 용어
- bh(x) : black-height, leaf까지 내려가며, path에서 black의 수
- 특징
- height bound : h ≤ 2 lg (n+1)
- complexity : O(lg n)
- 기능
- insertion : BST 방식으로 삽입 후, Fix
- uncle 색 따라 case 분류

- Deletion : BST 방식으로 삭제 후, Fix
- 삭제하는 것이 black일 땐, 대체로 큰 문제 x
- Red는 Fix 필요
-
sibling 따라 case 분류

- insertion : BST 방식으로 삽입 후, Fix