[Algorithm] 자료구조1 : Graph, Binary Tree, Heap, Priority Queues

Graph

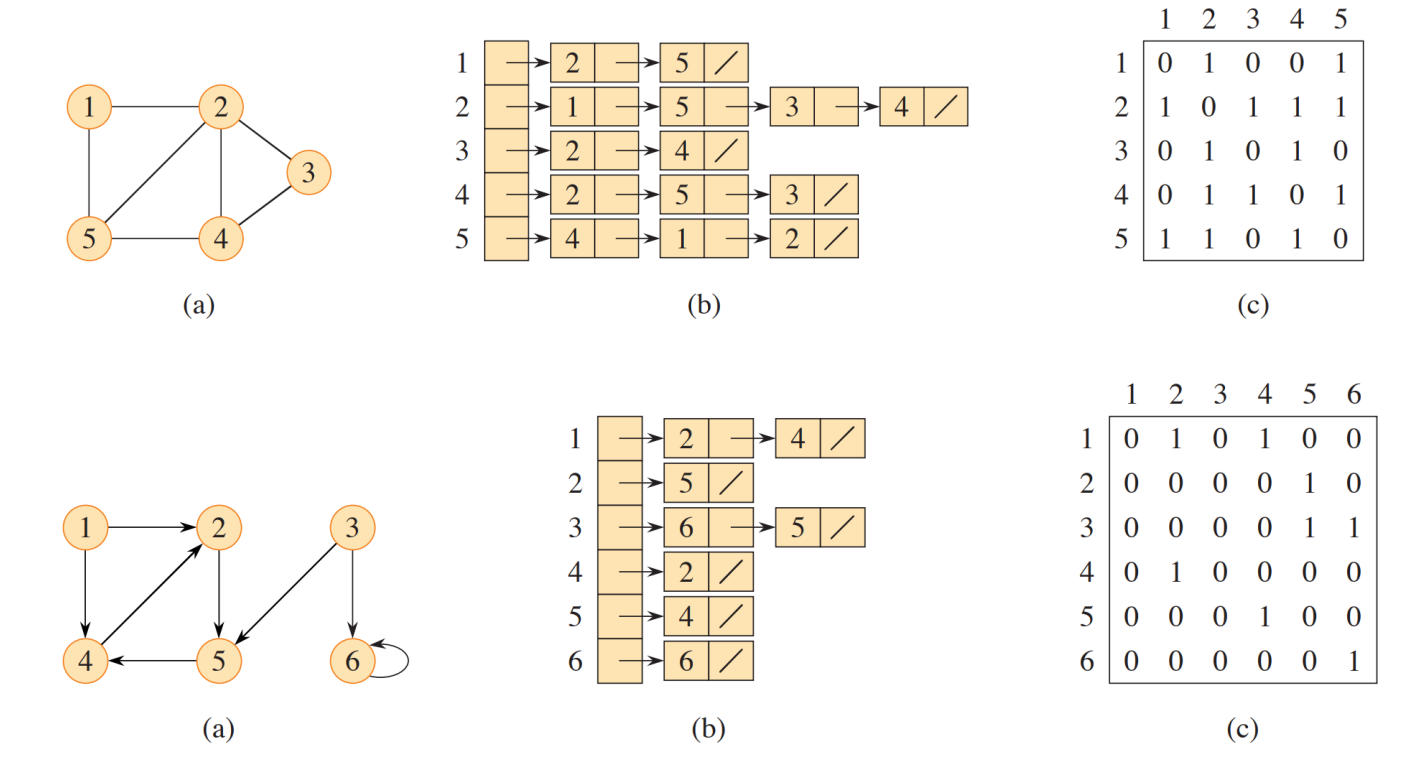
• 표현법
  • (b) : linked list

    • memory size :

      V

      +

      E

  • (c) : matrix

    • memory size :

      V

      ^2

    • 구현 쉽지만

      v

      커지면, 너무 Memory와 수행 시간 커짐

Binary Tree

• 자식이 0~2개인 Tree

용어

• degree : 자식 노드 수
• external node : leaf 노드, degree = 0
• interneal node : leaf가 아닌 노드, degree > 0
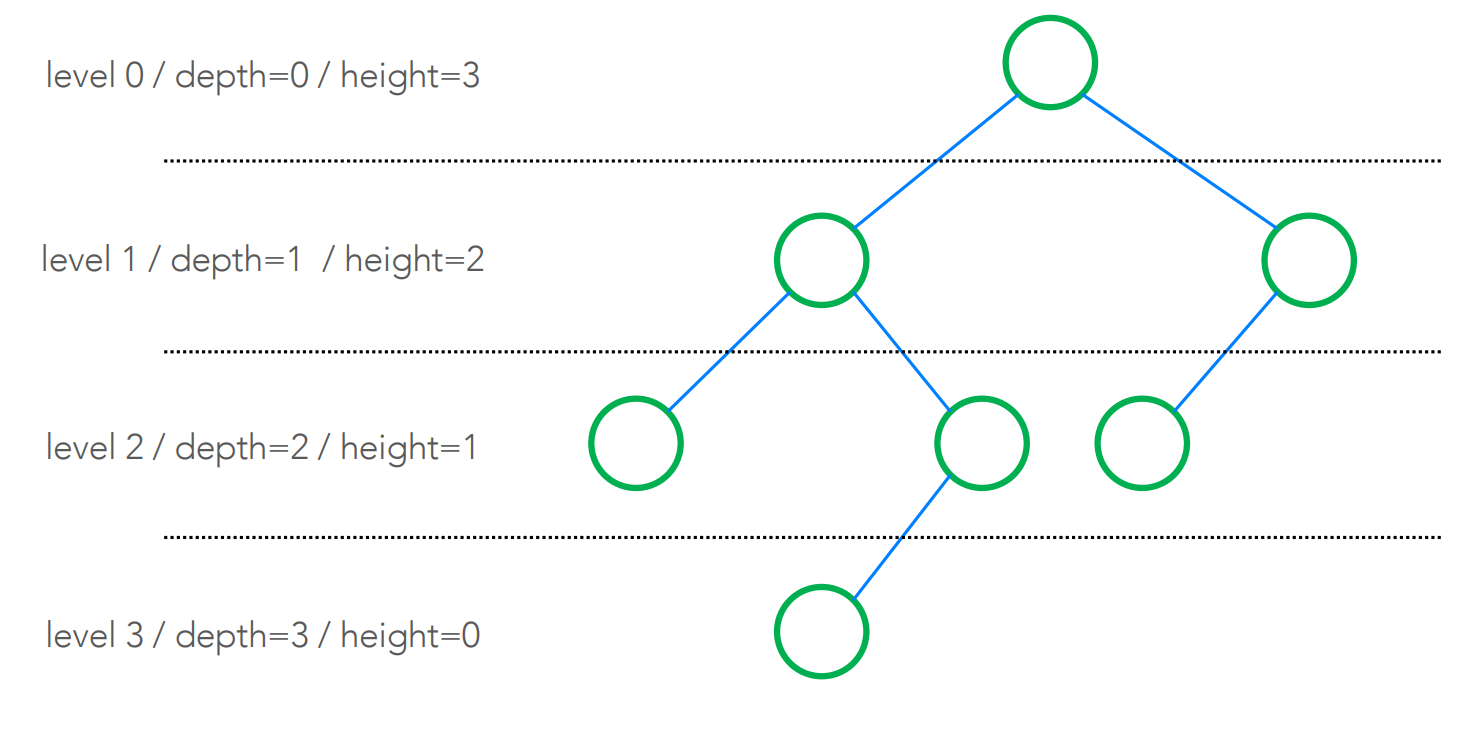
• depth : root까지 최단 거리 (=level)

• height : leaf까지 최단 거리

  

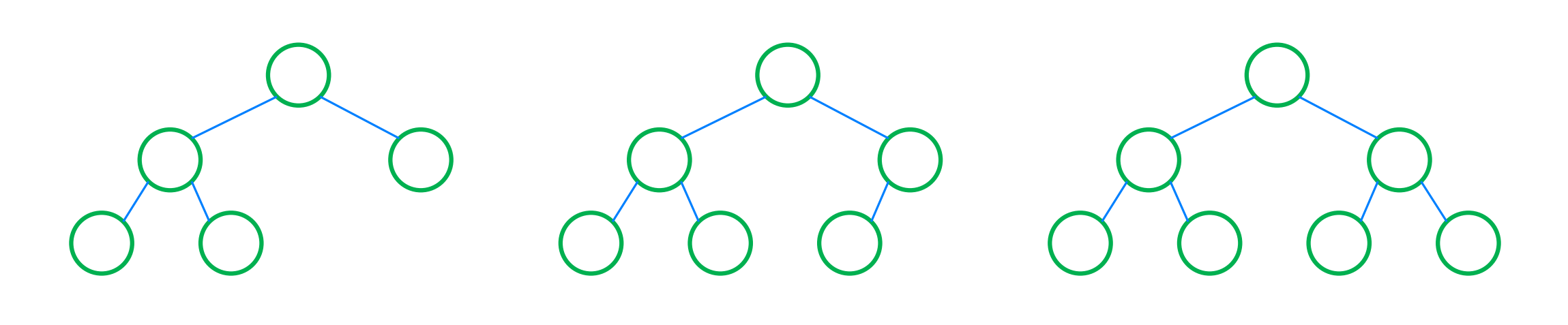
종류

• Full Binary Tree
  • 자식은 없거나 2개

  

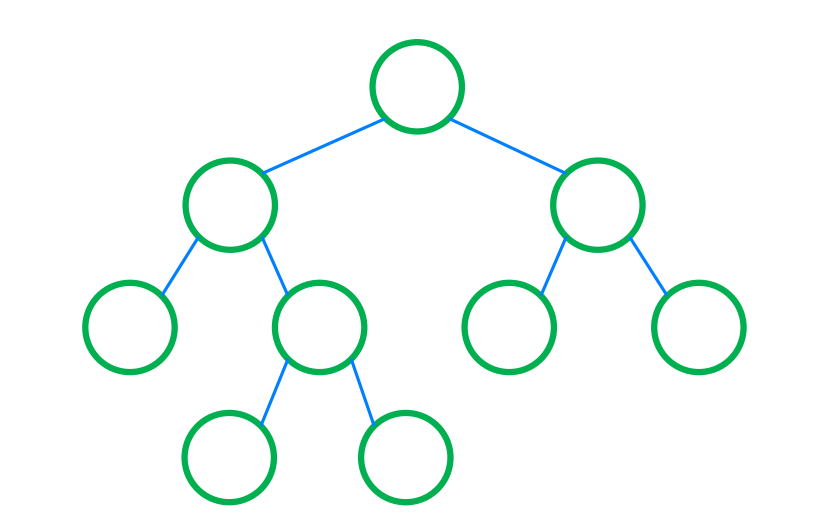
• Perfact Binary Tree
  • 자식은 없거나 2개 + 모든 level의 깊이 같다.

  

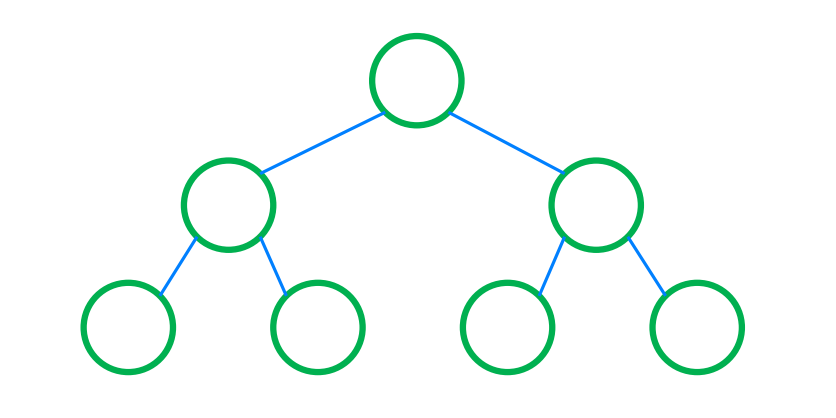
• Complete Binary Tree
  • 왼쪽 위부터 차례로 채운 형태
  • height h = floor($log_2n$)

  

Heap

• 왼쪽 위부터 차례로 저장하는, Complete binary Tree

  

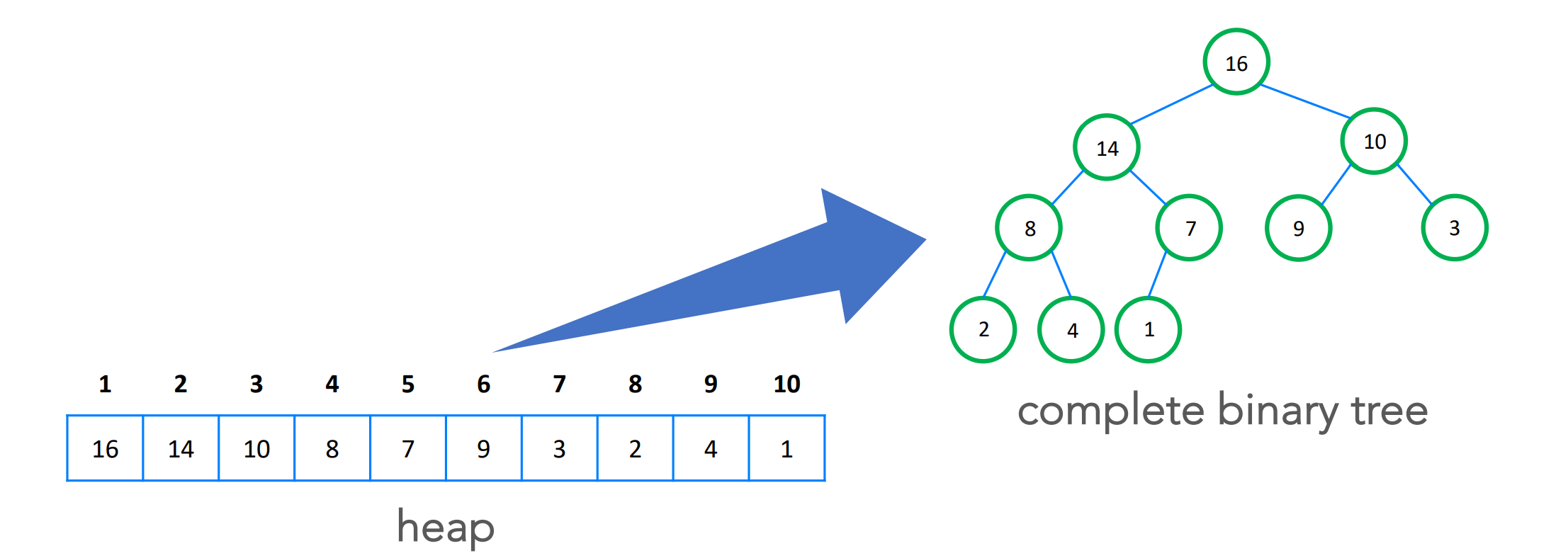
• 구성 요소
  • heapsize : 포함한 element 수
  • parent : return floor(i/2)
  • left child : return (2*i)
  • right child : return (2*i + 1)

• 코드

  

• 종류
  • Max-heap : 위로 갈수록 크다.
  • Min-heap : 아래로 갈수록 크다.
• 기능
  • MAX_Heapify : Max heap 되게 만들기

    • leaf까지 타고 내려가며, 자식 중 더 작은 것과 swap

      

    • complexity : O(h)

      • 증명있다고 하시는데… 그냥 아래로 타고 내려가니 높이 만큼 실행하니 당연한 듯.
  • Build Max Heap
    • bottom-up으로 max_heapify 호출
    • 뒤에서부터 볼 때, leaf 아닌 첫 노드(floor(n/2))에서 시작
      • leaf는 이미 maxheap 상태라고 볼 수 있다.

      

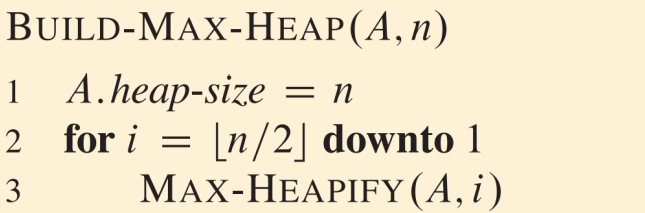
    • O(n) 정도 시간 걸림
      • 중간에서 호출하는 max-heapify들은 높이가 전체 tree의 height 아님.
• Heapsort
  • 1) max heap 만들기
  • 2) 아래 반복
    • root를 출력
    • 맨 뒤 노드부터 하나 씩 root랑 바꾼 후, root에서 max-heapify

Priority Queues

• 들어온 순서 대신, 부여한 우선순위대로 나가는 Queue
• heap과 key(priority) 사용
• 여러 operation들이 다 O(lg n)
• 기능

  • maximum(S) : largest key 갖는 element 찾기

    

  • extract_max(S) : largest key 갖는 element를 dequeue
    • 맨 마지막 노드를 root로 올린 후, Max-heapify

    

  • increase_key(S, x, k) : element x의 key를 k로 바꾸기
    • 부모랑 비교해서 swap하며, root까지 타고 올라가기
    • increase라서 k > x.key 이어야 함(반대로 decrease도 같이 만들수도 있음)

    

  • insert(S, x, k) : key k를 갖는 x를 enqueue
    • 마지막 위치에, - $\infin$ key로 넣은 후, increase_key