[Algorithm] All Pairs Shortest Path : Dijkstra, Bellman-Fold, EXTEND-SHORTEST-PATHS, Floyd-Warshall
- 구성
-
input : edge weight matrix W (n*n)
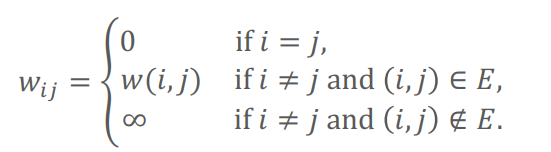
-
예시
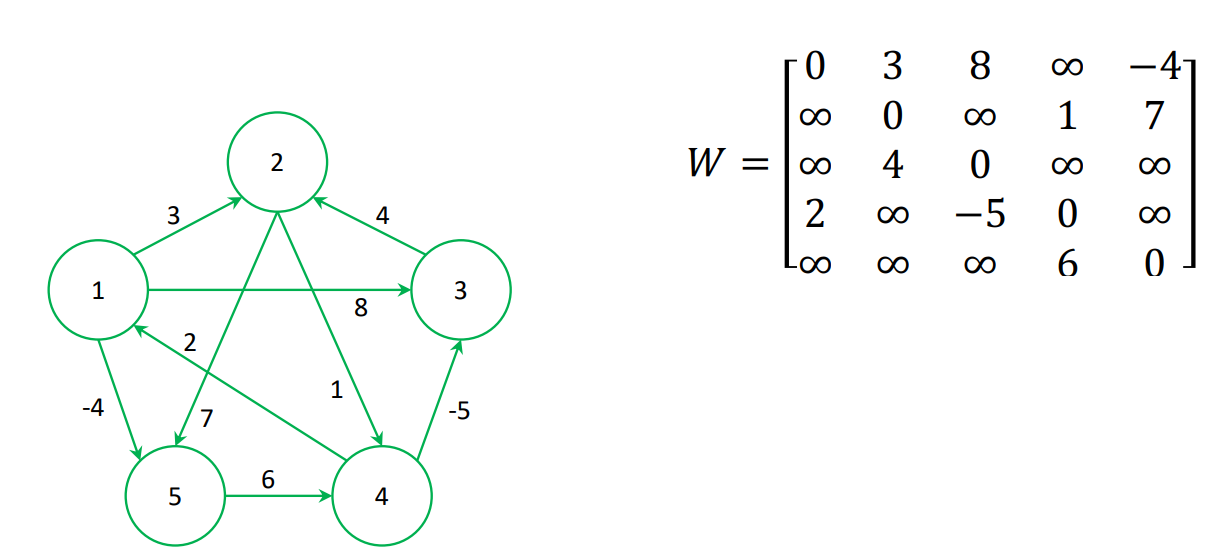
-
-
Output : shortest path weight matrix L (n*n), shortest path에 따른 parent node matrix
-
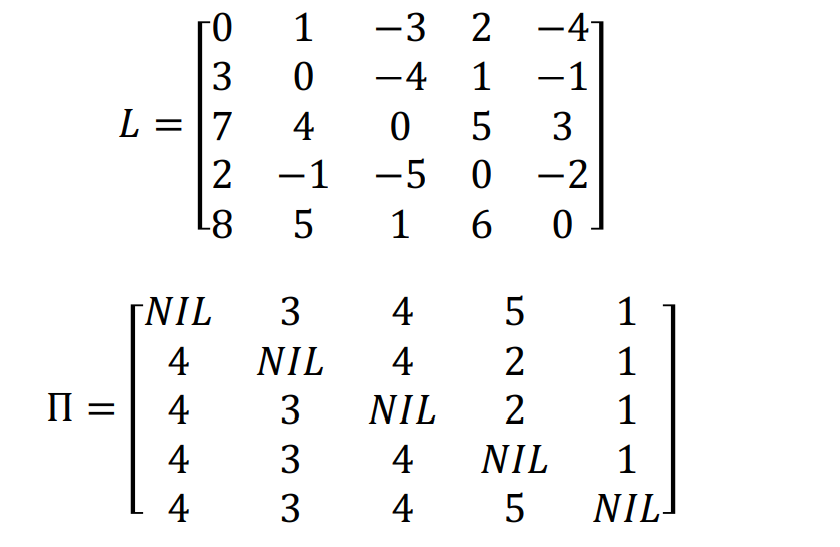
-
output으로 shortest path 출력

Dijkstra’s Algorithm 활용
- single source 용 shortest path를 찾는 Dijkstra Algorithm을 vertex별로 모두 실행
- complexity : O(V * (V+E)lgV) → O(V^3 lg V)
- dense graph 기준(sparse 하면 시간 감소 예상)
Bellman-Fold Algorith 활용
- 마찬가지로 single source 용 Bellman-Fold를 vertex 별로 모두 실행
- complexity : O(V^4)
EXTEND-SHORTEST-PATHS 활용
- 개념
- path p가 최대 r개까지의 edge만 가질 수 있다고 가정하자.
- i→j인 path p를 i→k→j (p’ : i→k)로 나누기
- p’도 shortest path
- p’는 최대 r-1개의 edge 가질 수 있음
-
i→j까지 r개 이내의 edge로 이동한 최단거리 = min( k 노드까지 최대 r-1 번의 edge로 이동한 최단거리 + k→j의 weight (1≤ k ≤n인 모든 k에 대해))
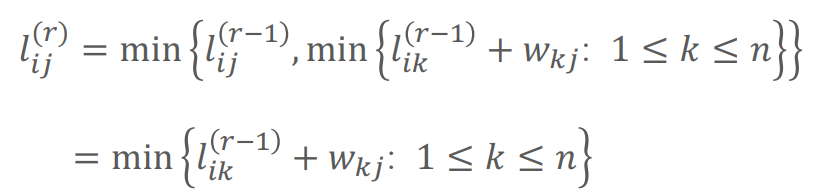
- recursively 진행. r ≥ n-1에서 종료
- 방법
-
if r=0 : base setting
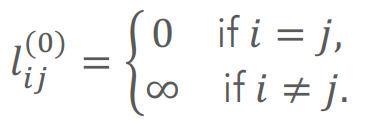
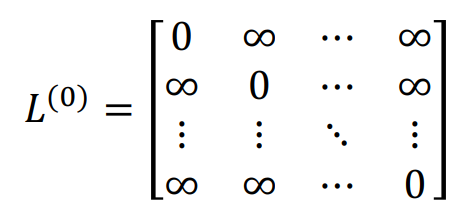

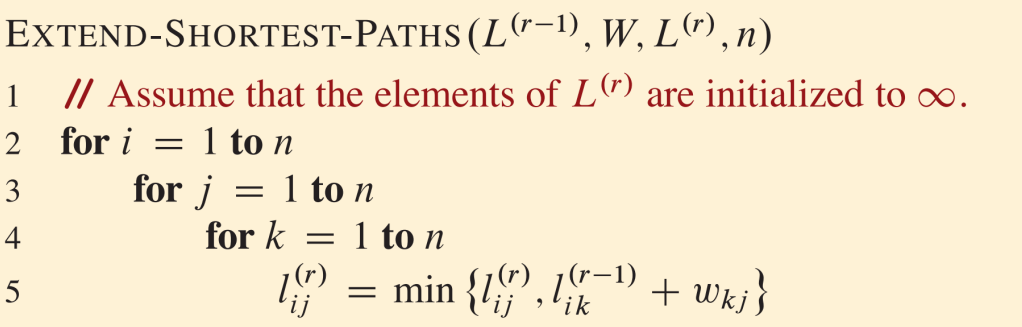
- 이전 타임까지의 각 노드까지의 best case에, 각 노드에서 목적지까지 이동 weight를 더해서, min
- complexity : $\theta(n^4)$
-
- Max Form 사용
-
matrix multiplication 대신, element간 합 → ,min을 사용한다.
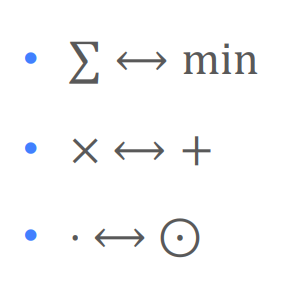
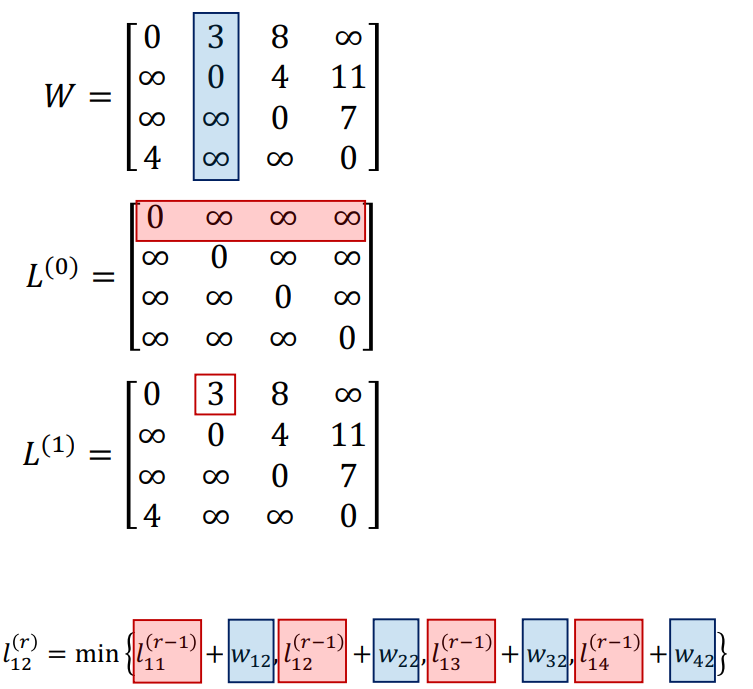
-
- Dynamic Programming
- $L^0$ initialize 이후, w만 쌓아가며 모두 계산 가능
- $L^0$는 identity matrix 같은 역할을 하게 된다. 따라서 $L^n$ = $W^n$ 이 된다.
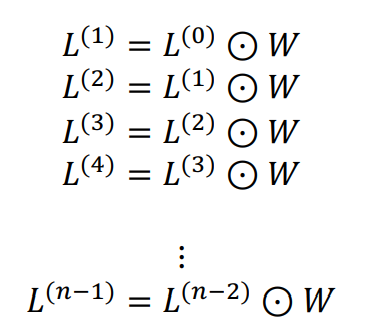

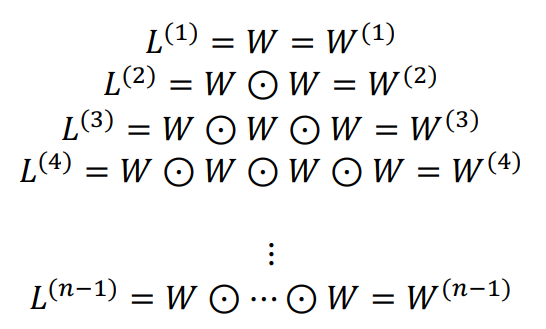
- exponentially 접근 가능
- r ≥ n-1 일 때는 모두 서로 동일(이미 최단 거리 계산 끝)
- 따라서 정확히 n-1일 때 찾을 필요 없이, r ≥ n-1 되면 멈추기만 하면 된다.
-
따라서 log n 번만 곱하면 된다.
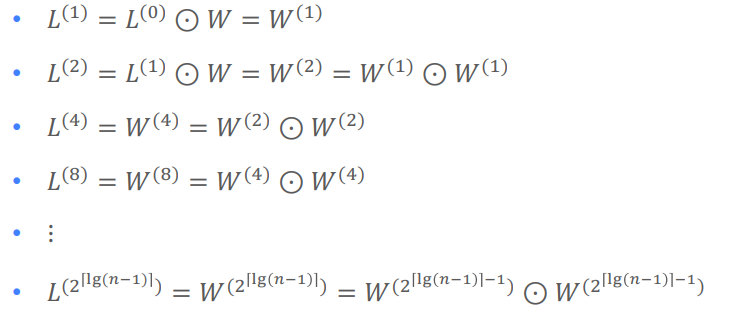

- complexity : $\theta(n^3lg n)$
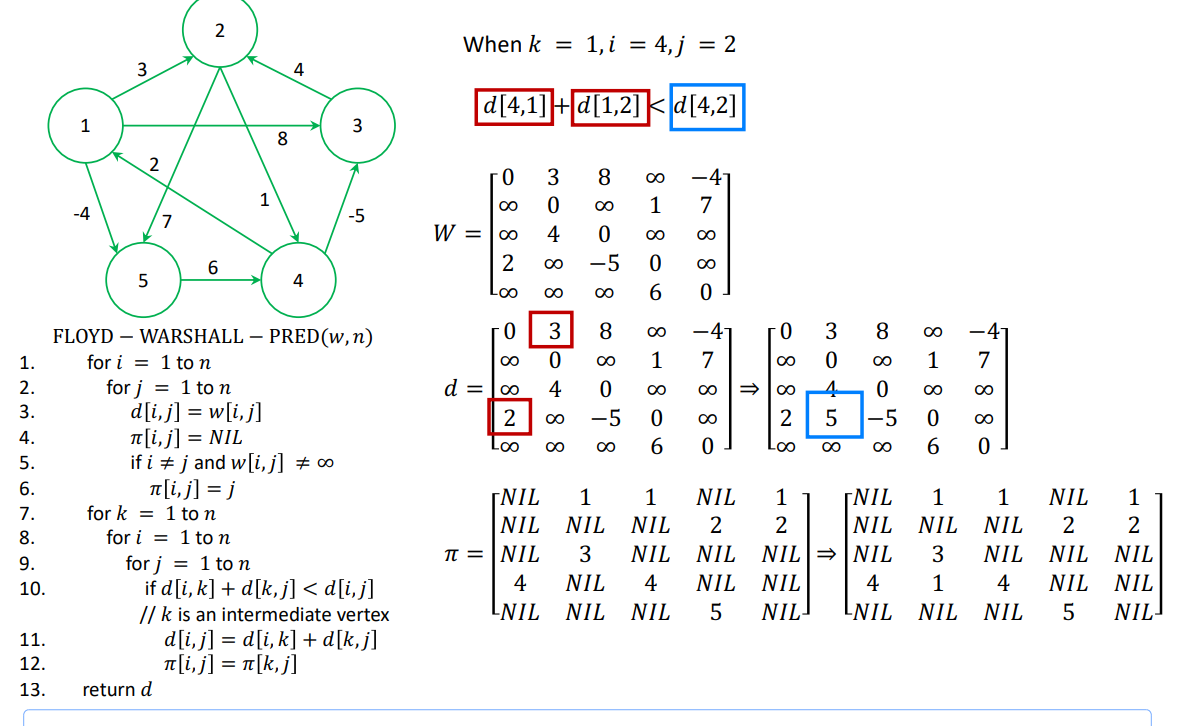
Floyd-Warshall Algorithm
- complexity : $\theta(V^3)$
- intermediate vertex들은 $\in$ set {1, 2, 3, …, k}라고 가정
- 1~k vertex는 intermediate에 있을 수도 있고, 없을 수도 있다.
- k+1 vertex는 intermediate 아님
-
- intermediate vertex : path p 속 노드 중, 시작과 끝을 제외한 노드들
- 방법
- i→k→j에서, intermediate vertex로 k를 포함하는지에 따라 나눈다.
- case1) k 포함 : $d_{ij}^{(k)} = d_{ij}^{(k-1)}$
-
case2) k 포함 x : $d_{ij}^{(k)} = d_{ik}^{(k-1)} + d_{kj}^{(k-1)}$
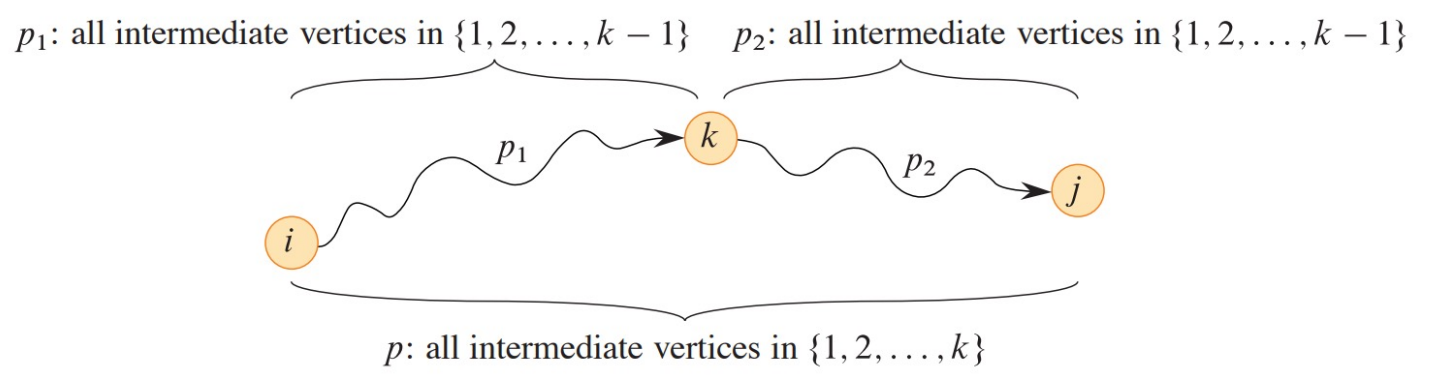
- 최종 $d_{ij}^{(k)} = min{d_{ij}^{(k-1)}, d_{ik}^{(k-1)} + d_{kj}^{(k-1)}}$
- 최적 path 찾기(not only weight) : parent 활용
- best direction이 update될 때, parent도 update